Notes on 3D
Three dimensional objects are defined in computer graphics as collections of points or vertices, either connected by edges or grouped together in polygonal faces. Displays of edges are called wire-frame displays, are relatively simple to do and are fast to display, rotate, move, etc. Filled-in faces take more time, are a little more difficult to implement, but can look much more realistic. This hand-out will focus on wire-frame displays. Later we well look at filled 3D objects.
3D Coordinates System
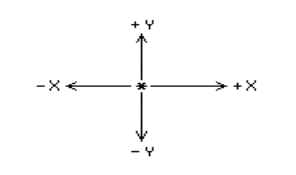
3D graphics uses three dimensional coordinates X, Y, and Z-axes. The X and Y axes are the two-dimensional ones we are already used to. The Z axis is perpendicular to them. In the figure below, the X and Y axes are labeled, and the Z axis passes through the paper, where the ( * ) is:
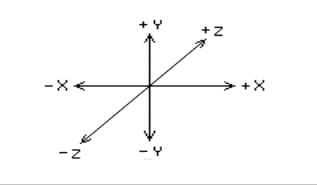
A perspective view of the Z axis is shown in the figure below:
The viewer is considered to be a single eyed, whose eye is located at the origin -- where X, Y, and Z all equal 0. We will be using what is known as a left-handed coordinate system -- in which:
X gets larger to the right,
Y gets larger going up,
Z gets larger going to the front (into the paper).This means that negative Z coordinates are behind the viewer, positive Z coordinates are to the front of the viewer. A point at (50, 60, 70) would be 50 pixels to the right, 60 pixels up and 70 pixels forward, (into the paper.) A point at (20, -15, -90) would be 20 pixels to the right, 15 pixels down and 90 pixels behind the eye (that is behind us.)
Projection
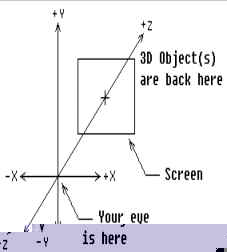
The major problem of wire-frame 3D is getting an object in 3D space to fit, that is to display, on a 2D screen -- how does one project a solid object onto a plane? Think of the viewer as looking through a window located some distance down the Z axis, that is into the paper, right in front of us. This window is the screen, which coincides with the actual video screen a real viewer will look at. The Z-axis passes through the center of the screen. The edges of the screen are paralleled to the X and Y-axes. Think of an object in the 3D space on the other side of the screen from the viewer. That is, the eye is in front of the screen and the screen is in front the object.
"Light-rays" travel form the vertices of the object, through the screen and to the viewer's eye. If we could see the light rays piercing the screen, we could mark those places on the screen with spots. If we connect these spots with lines in the correct order, that is in the order that we connected them when we define the shape, we would have a nice perspective drawing of the object. Every 3D program needs to have a projection function. This function requires the X, Y, and Z-coordinates of each point and the distance of the screen from the viewer. The results are placed in another set of X and Y arrays, which are used for the display. The secret of projection is based on the obvious fact that objects appear smaller when they are farther away and larger when they are closer. It would seem that dividing the X and Y-coordinates of the object by the Z-coordinate in some way would make the resulting projection smaller when the Z is large (the object is far away) and make them larger when the Z is small (the object is nearby.) The resulting function works as follows:
projected_x = x * screen_distance / z projected_y = y * screen_distance / zfor each point. Fortunately, when we project a straight line, the projection is also a straight line. So we only need to project the end points and connect them with a straight line.
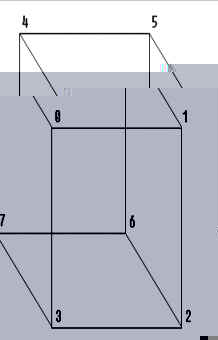
The examples programs all work with a cube, because its a common form, and it is very easy to figure out its X, Y, and Z-coordinates. It has eight corners or vertices, but has 12 edges. This is a little more difficult than drawing 2D outline -- we just can't connect the points in order. Instead, we have to tell the program the order to connect them. We can think of the vertices as being numbered form 0 to 7 -- they are stored in arrays from coord[0][X] to coord[7][X], coord[0][Y] to coord[7][Y], etc. Note that X and Y are pre-defined like:
final int X = 0; final int Y = 1;An array of edges should have two numbers, each representing the index of a vertex. On the cube below, the 12 edges are:
0-1 1-2 2-3 3-0
0-4 1-5 2-6 3-7
4-5 5-6 6-7 7-4
Probably (this is true in most cases) the hardest part of doing 3D graphics is figuring out how to connect the edges.
Movement
The three transformations of 3D graphics are translation (movement), scaling, and rotation. We will deal only with movement in this lecture. To move an object, create a three element array trans[], for the amount to move along the X, Y and Z axes. This array and the coordinate arrays are trans[] array are each added to the corresponding X, Y and Z-coordinate for each vertex in coord[][]. When moving 3D objects around, it is easy to go off the screen with the projection. In particular, if the object gets too close to the viewer. Also there is a danger of having Z coordinates equal to zero. Since projection requires dividing the screen distance by the Z-coordinate, this could result in a termination of the program caused by a "division by zero" error. We must always make sure that a vertex is in a safe location before projection. In the demo programs, the values in the coord[] arrays are chosen and kept in limits so that they will always have 2 coordinates greater than 0. So no test is necessary.